
Turbo codes were invented by C. Berrou, et al., in 1993. It has excited the coding community with the promise of performing near channel capacity by using an iterative decoding technique that relies just on simple constituent code. Because the interleaver, the code appear to be long and random, thus emulate the good performance of the random codes. Conventional turbo codes are parallel concatenated recursive systematic convolutional codes. Two convolutional encoders are connected by a large enough random-like interleaver, which is shown in the following diagram:

the output of two encoders need to be punctured to keep the rate=1/2.
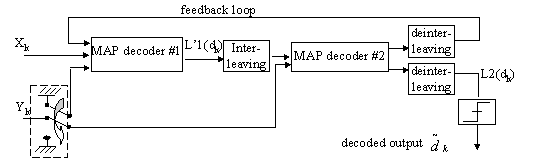
Viterbi algorithm is a native ML (maximum likelihood) decoder which minimizes the probility of sequence error for convolutional codes. Unfortunately, this algorithms is not able to yield directly the APP for each decoder output. Furthermore, because of the existence of the interleaver, the code trellis structure becomes very complex, it’s very hard to decode it directly. So the turbo code applies iterative decoding which use the output APP of one decoder as extrinsic information to the next decoder. The diagram of the decoder is dipicted in the following figure:
A relevant algorithm which can output APP for each bit was proposed by Bahl et al. in 1974. This algorithm minimizes the bit error probability in decoding linear block and convolutional code and at the same time, output the APP for each decoded bit. For RSC code, the Bahl algorithm must be modified in order to take account their recursive character.
The MAP decoding is the method that tries to find the maximum P(dk=i|R), a posteriori probability (APP) for each information bit, R=RN1 is the received sequence. The hard decision is made on the APP:
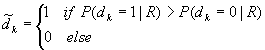
Using the Bayes rule, the APP can be expressed as:
![]()
where the Sk is the encoder state of time k, dk causes the encoder transferred to Sk from Sk-1. The encoder state is assumed beginning with S0=0. Please note that in this notation, Sk indexes from 0 to N, dk indexes from 1 to N.
The above equation can be re-write as follows:
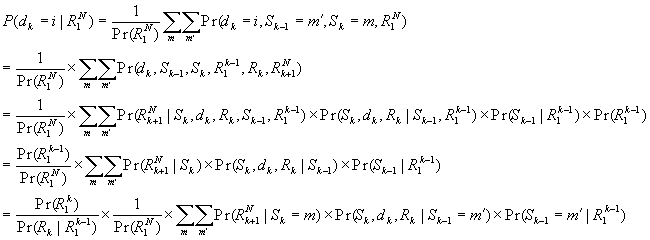
Let
![]()
The above equation becomes
![]()
The coefficient of the sum is a constant to every fixed k and can be fixed when normalizing
Please note in these equations, dk = i force encoder state transfer from Sk-1 to Sk, so the index of information sequence d should be from 1 to N, S then from 0 to N. Of course we assume that the encoding beginning from all zero state, that is, S0=0.
The encoding process is depicted with the following diagram:
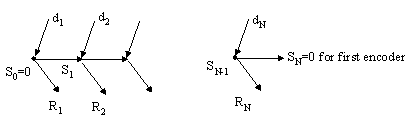
a , b items can be recursively defined with g :
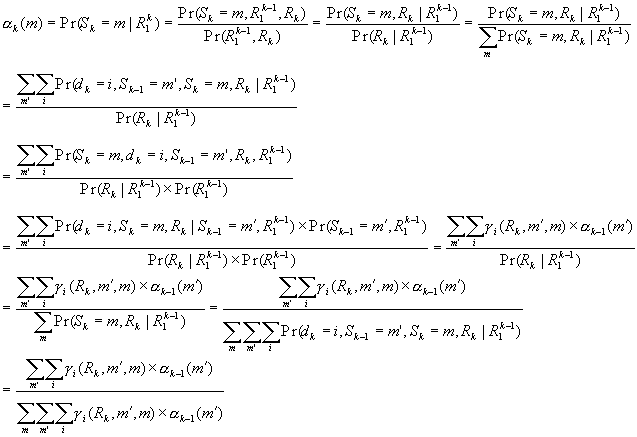
g is a function of encoder state Sk-1, input d at time k and received symbol R at time k. Of course it can also be defined as a function of Sk, dk and Rk.
The same deduction comes to b :
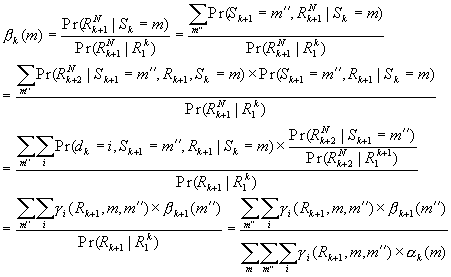
The denominator of last equation comes from the deduction of a.
One must be aware that a indexes from 0
to N, b indexes from 1 to N, and g indexes from 1 to N. Input sequence dk
also indexes from 1 to N. This is important for programming. g is better programmed as a function of dk, Sk(not Sk-1),
and Rk for better understanding.