1. Basic topics

(1) Decimation and Interpolation

In most applications, the decimator is preceded by a lowpass digital filter called the decimation filter. The filter ensures that the signal being decimated is bandwidth limited.

Next, an interpolation filter is a digital that follows an expander. The typical purpose of the digital filter is to suppress all the images caused by the expander.

The relationships of the input-output are:

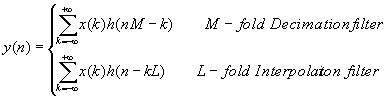
in time-domain, and

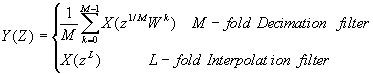
in frequency domain.

(2) Some special filters

1. power complementary filters:

M transfer functions H_k(z) are said to be power complementary if



2. Mth band filter

A filter is said to be an Mth band filter (or Nyquist(M)) filter, if the impulse response h(n) satisfies

Above equation implies that . So we can conclude that all these M uniformly shifted versions of Mth band filter H(e^jw ) add up to a constant.

(3) Noble Identities

We can interchange the positions of interpolator (decimator) and filters with the noble identities

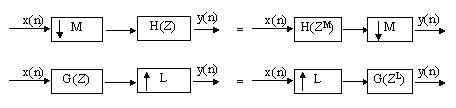
(4) Polyphase Decomposition

An important advancement in multirate signal processing is the invention of the polyphase representation of a filter:

The impulse response of the k^th polyphase filter G_k(z) is simply a subsampling of h(n+k):

This can be viewed as the following diagram:

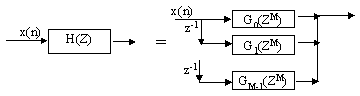
Actually if the filter H(z) is followed by a decimator, then according to the noble identity, the decimator can be located before the poly-filters, i.e.,

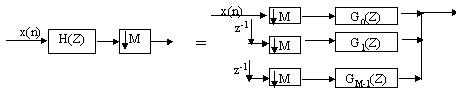
The total computation load is the same as the original H(z).

Similarly, if a expander is in front of H(z), the expander can be moved to the right-side of the polyphase decomposition of H(z), to keep the total computation load is also the same:

1. Paraunitary PR filter banks

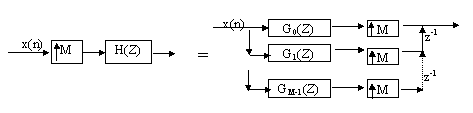
The general maximally decimated filter bank decomposition is showed as following:

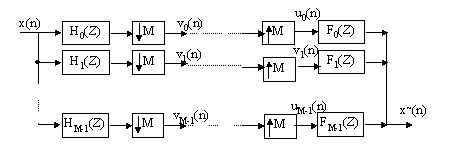
let:

We can express the reconstructed signal as:

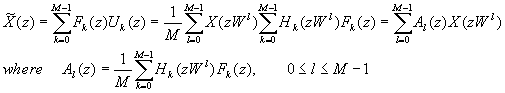
The items which l¹ 0 represent shift versions of the spectrum X(e^jw ). So the reconstructed signal is a linear combination of X(e^jw ) and its M-1 uniformly shifted versions. Furthermore, we can rewrite the above expression of A_l(z) as:

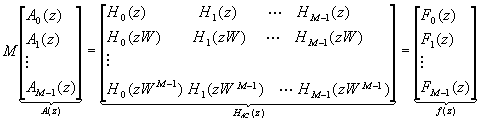
To cancel aliasing, we have to force all elements on the left side of above equation to zero except the top element. So the conditions for alias cancelation can be written as:

So it is clear that, given a set of analysis filters Hk(z), we can in principle cancel aliasing by solving for the synthesis filters as . This works as long as [detH_AC(z)] is not equal to zero. Of course we can go further and obtain the perfect reconstruct, simply by requiring that t(z) be of the following form:

Another way to construct the PR filter banks is using polyphase decomposition. We can express H_k(z) in the form:, then rewrite this H array as:

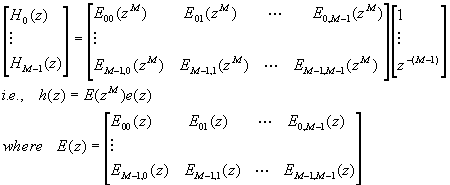
is the M´ M type 1 polyphase component matrix for the analysis bank. The left part of the following figure shows the idea pictorially. The right part shows the case of synthesis banks

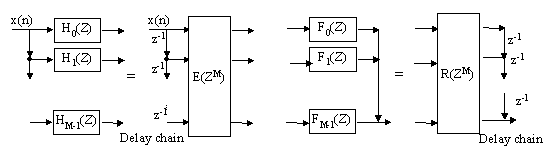
In an similar manner we can express the set of synthesis filters, i.e., by type 2 polyphase decomposition,

Express above equation using matrix notation we have

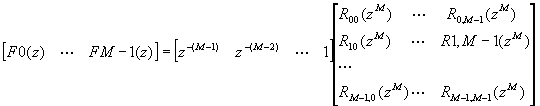
In terms of e(z) and synthesis-bank vector f(z), this becomes:

where matrix R(z) is type 2 polyphase matrix for the synthesis bank.

Now combine the two polyphase decomposition and using the noble identities to move the expanders and decimators, we get the following diagram:

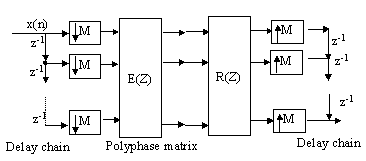
Finally, we can combine the matrices and get a M´ M matrix P(z) :

The necessary and sufficient condition for the perfect reconstruction (PR) is:

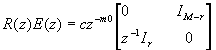
for some integer r with 0£ r£ M-1. And it holds whether the system is FIR or IIR.

One sufficient (but not necessary) PR solution for the above filter banks is we choose E(z) to be paraunitary, i.e., and for some fixed constant d. The paraunitary property implies. . So if we choose R(z) as for some c¹ 0, the PR condition can be satisfied. Neither c nor K is fundamental but choice of a positive K serves to ensure that R(z) [hence F_k(z)] is causal.

The Paraunitary constrain enables us to construct synthesis filter banks easily from the analysis banks. That is,

There are several important properties caused by paraunitary solutions:

1. 
2. power complementary property:
3. Each H_k(z) is a spectral factor of a (zero-phase) Mth band filter. In other words, the filter D_k(z) defined as is an Mth filter.
4. H_AC(z) is paraunitary iff E(z) is paraunitary, and then we have the conclusions on time-domain:



5. The paraunitary solution for M=2 band filter banks is the one satisfies the interscale equation of wavelet construction.

1. Relationship between filter banks and orthonormal filter banks

Orthonormal transform (including LOT, lapped OT) is a special case of filter banks. We may extract the delay elements of E(z) and R(z) to the delay chains and re-arrange the signal flow as:

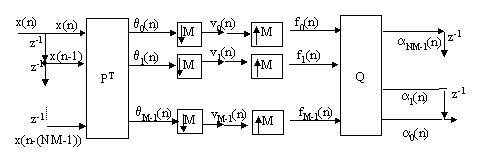
where NM is the length of the filters of the bank. Actually this can be viewed as a transform with matrix P^T, N=1 is the normal orthonormal transform, N=2 is the case for LOT.

We then define input vector, and partition it into N blocks of M samples each as follows:

The input vector is multiplied by P^T to get the coefficient vector

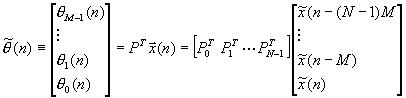
where each P_k^T is a M by M block. This can be written as

Because of subsampling (decimation) by M, every M new input samples are entered into the delay chain and then output v is calculated once.

Define , we then have

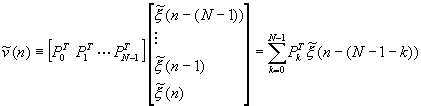
This is like a block FIR filter, whereas the filter coefficients are the (M by M) matrices and the signals are (M by 1) vectors . After N-1 samples at the slow clock rate (i.e., (N-1)´ M original clock rate), there is an entirely new data vector in the input delay chain (buffer). Stacking the successive output, we get (starting at n=0 for convenience):

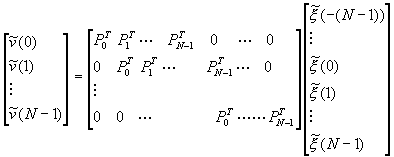
To relate this representation to the filter bank structure, we can write

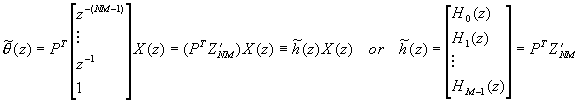
where the delay vector Z’_MN is and , r=0,1,…,M-1

This equivalence state that the block transform for x to q can be replaced by the analysis bank h, where the length of each filter is NM. Then we can obtain the polyphase representation of block transform, they have the following relationship:

now moving the decimator to the front of filter banks, we get:

Every element in matrix E(z) is a polynomial in Z^-1 of degree N-1. Therefore we can express E(z) with matrix coefficients:

each E_pk is a constant (no z^-1 items), M´ M matrix and related with block transform with the following equation:

The synthesis (receiver) bank can be deducted in a similar way.