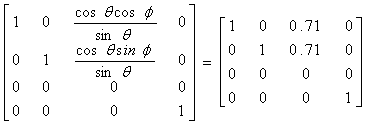Tutorial 5

CSC204/CPE411/SC20 Tutorial 5

Viewing in 3D

Solutions

1. What projections are known as planar geometric projections? Describe the subclasses for the planar geometric projections.

If the projection is onto a plane rather than some curved surface and the projection rays (called projectors) are straight rather than curved, the projection is called a planar geometric projection.

Planar geometric projections can be divided into two basic classes: perspective and parallel.

If the distance between the Centre of Projection (COP) to the projection plane is finite, the projectors are not parallel to each other. This kind of projections is called perspective projection. Perspective projections are further subdivided by the number of vanishing points, thus called 1-point, 2-point, or 3-point perspectives.

If the distance between the COP and the projection plane is infinite, the projectors are parallel to each other. This kind of projections is called parallel projection. Parallel projections are categorized into two types, depending on the relation between the Direction of Projection (DOP) and the normal of the projection plane. In orthographic projection, the projectors are perpendicular to the projection plane. In oblique projection, they are not.

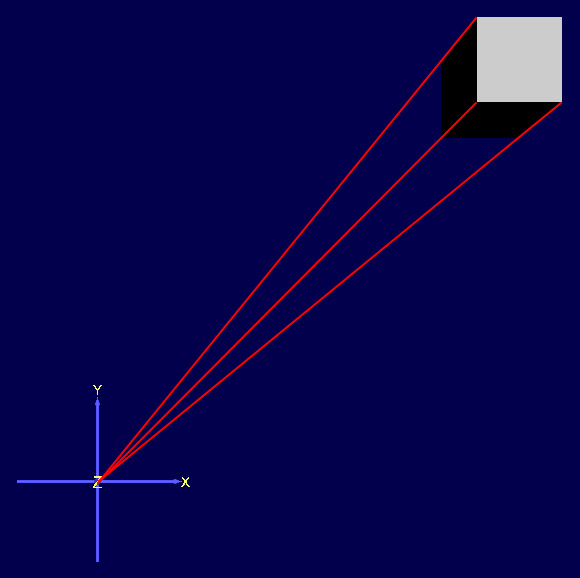
Click at the figure to see a VRML demo. This demo illustrates how a perspective projections can be changed to parallel projection by moving away the observer and reducing the field of view angle.
Press PageDown button when seeing the scene to move between the viewpoints. The first viewpoint will position the observer in front of the unit cube and 2 meters away from it.
Viewpoint {
   description "Perspective projection"
   position 0 0 2
   fieldOfView 0.784999
}
We can see that the cube is projected with a perspective distortion. Next, when PageDown is pressed, the viewpoint is moved 1000 m away from the cube. The cube then is seen as only a single dot on the screen.
Viewpoint {
   description "Parallel orthographic projection"
   position 0 0 1000
   fieldOfView 0.784999
}
Next, by pressing PageDown again, we reduce the view angle from 0.784999 rad to 0.0012 rad and see the cube as if it is projected with a parallel projection.
Viewpoint {
   description "Parallel orthographic projection"
   position 0 0 1000
   fieldOfView 0.0012
}

2. How to perform an orthographic projection of some 3D objects onto the projection plane which contains the y-axis and has a 30° angle with the z=0 plane? Derive a single matrix of the transformation.

The projection plane is located as follows:

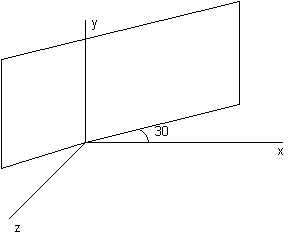
To apply the matrix of orthographic projection onto the plane xy, we have to rotate the objects to be projected about the y-axis by -30. So, the combined transformation is

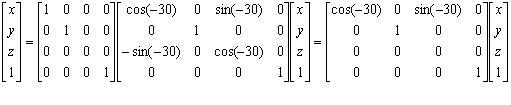
It is essential that we must not do any inverse rotation. We are interested in obtaining 2 coordinates on a plane. To achieve it, we moved the projection plane and the objects to be projected so that the projection plane becomes one of the coordinate planes. After this we project onto the coordinate plane and consider the respective 2 coordinates. In case of this example - these are coordinates x and y.

If the question is about perspective projection, the transformation must be such that it moves the projection plane to become one of the coordinate planes, and the centre of projection on the respective coordinate axis which is orthogonal to the coordinate plane.

3. Consider an origin-centered unit cube. Translate the cube 5 units in the x and y directions and perform a single-point perspective projection onto the z=0 plane from a center of projection at z=10.

The position vectors of the origin-centered unit cube are

The concatenated transformation matrix is

The resulting transformed position vectors are:

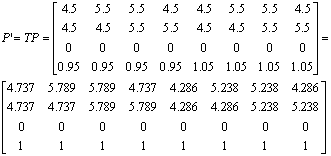
4. A unit cube is centered at (0, 0, -0.5) and its three sides are parallel to the X, Y and Z axes respectively. Find its projected image on the X-Y plane when (i) DOP = (0,0,-1), (ii) DOP = (0,-1,-1) and (iii) DOP = (0,-1,-2). What types of projection are they?

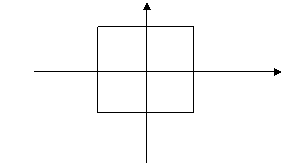
(i) When DOP=(0,0,-1), the projection is an orthographic projection from the front. The projected image is the square bounded by (-0.5, -0.5,0), (-0.5, 0.5, 0), (0.5, 0.5, 0) and (0.5, -0.5, 0).

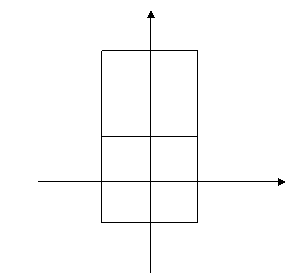
(ii) When DOP =(0, -1, -1), the projector is having a 45°angle with the projection plane. This is a cavalier projection. The projected image is as shown in the figure below.

(iii) When DOP= (0, -1, -2), the projector is having a 63.43° angle with the projection plane. This is a cabinet projection. The projected image is as shown in the figure below.

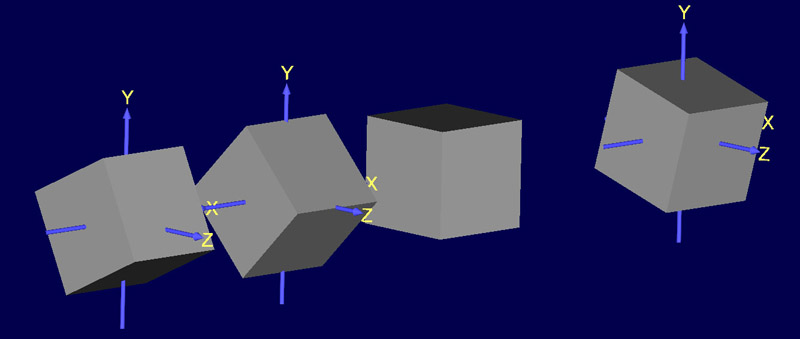
Click on the figure to see a VRML scene illustrating this question. Instead of changing the DOP vector, the cubes on the left were rotated about axis X
by 45° and 63.45°. The cube on the right continuously rotates about axis X. Examine the scene by moving it around with a mouse.
You can also change the graphics mode to "Smooth".

5. Derive the viewing transformation matrix of the oblique projection onto the x-y plane as shown in Fig Q4.

First, find the direction vector of the projector V. From the above figure, for a unit vector along the projector direction, its x, y, z components can be written as

x_V= cosqcosf y_V= cosqsinf z_V= -sinq

Hence the direction vector V of the projector is (cosqcosf, cosqsinf, -sinq).

Consider one arbitrary point P(x,y,z). It has been projected onto the XY plane at P’(x’,y’,0). The vector has the same direction as V and =kV. For point P’ we can write the following:

x' =x + k cosqcosf y’ =y + k cosqsinf 0 = z - k sinq

Hence k = z/sinq and

Recalling that q=f=45, the projection transformation matrix is then

Assuming a column represented position vector, write in a proper order individual matrices composing parallel orthographic projection onto a plane defined by equation x + y − 1 = 0. The final matrix is not required.

A parallel projection has a DOP = [-2 1 2] and its projection plane is the XY plane. It is applied to a point whose x, y, and z coordinates are all 6. Compute the coordinates of the projected point.