CSC204/CPE411/SC208 Tutorial 1

Graphics Systems and the Viewing Pipeline

 

 

Solutions

 

1.         Suppose we have a screen that can display 256 colours simultaneously and that is 800 by 600 pixels.

            (a)        How much memory is required to make full use of this display?

            (b)        If the screen has to be redrawn 60 times per second, at what rate must pixels be processed by the display processor?

 

(a)        To get 256 simultaneous colours, each pixel would have 8 bits because 256=2⁸.

Total memory bits required = 800*600*8 =480,000 bytes= 3,840,000 bits

In general, total memory bits required = Rx * Ry * 8, where Rx and Ry are the resolutions in the x, y-directions, respectively.

 

(b)        Number of pixels to update per sec = 800 * 600 * 60 = 28,800,000 pix/sec.

Read more about display resolution here.

 

2.         Consider a raster display system with a frame buffer of 1 Mbyte.

            (a)        What is the maximum number of colours, which can be displayed in this system if a resolution of 1024x768 is selected?

            (b)        Given the available resolutions of 640x480, 800x600, 1024x768, and 1152x864, suggest the maximum possible resolution for which we could display 16,777,216 colours.

 

(a)        The maximum number of colours is defined as follows

 

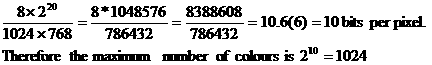
(b)        Since , 24 bits will be used for every pixel. Assuming that the aspect ratio is 1024/768=4/3, the resolution can be obtained as follows:

, which makes the resolution of 640x480.

 

Read more about frame buffers here.

 

3.         A color map is an important component of a graphics system.

            (a)        Explain when a colour map is necessary.

            (b)        What determines

                        (i)        the maximum number of colours? 

                        (ii)       the number of colors which can be displayed simultaneously?

                        (iii)      the number of entries in each colour map?

 

(a)        A colour map is necessary when it is required to have a large palette of colours, but a large frame buffer is not available. A colourmap is used to map a pixel value to a colour for display. The pixel value is used as an index into the colourmap. The entry in the colourmap determines the actual colour for that pixel by controlling the intensity of each visible RGB element.

 

(b)

(i)         The maximum number of available colours to select from is 2^m, where m is the number of bits per entry of the colour map.

(ii)        The maximum number of simultaneous colours is 2ⁿ, where n is the number of bits per pixel in the frame buffer. m >> n.

(iii)       The same as (ii). 2ⁿ colours are selected from 2^m colours, where 2^m.>> 2ⁿ

 

^{More about colour map (palettes) can be found here.}

4.         Briefly describe

(a)               World Coordinate System.

(b)               Device Coordinate System.

(c)                Modelling Transformation.

(d)               Window-to-Viewport Transformation.

 

(a)                The coordinates referenced by a user are called world coordinates or modelling coordinates. They are defined in the World Coordinate System (WCS) or Modelling Coordinate System (MCS) which is in turn defined in the WCS.

(b)               The coordinates used by a particular output device are called device coordinates. They are defined in the Device Coordinate System, which is usually a Cartesian Coordinate System.

(c)                Modelling Transformations transform the coordinates within the WCS or MCS. They are Affine Transformations (Translation, Rotation, and Scaling) and other Non-linear Coordinate Transformations.

(d)               Window-toViewport transformation transforms the coordinates from the WCS to the DCS using two rectangular bounding areas: a Windows in the WCS and a viewport in the DCS.

 

Read more about coordinate systems here.

3D Cartesian Coordinate system VRML model